EXPONENTIELLES
WACHSTUM:
Aufgabe 1)
Im Juli 2008 lebten im Hongkong nach Schätzungen 7 018 636 Menschen.
Das Bevölkerungswachstum beträgt ca. 0, 532
%. Wie viele Einwohner wird die Millionenstadt bei konstantem Wachstum in 20 Jahren haben?
Lösung:
| |
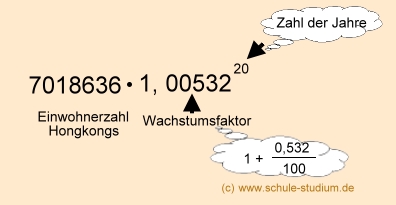
In 20 Jahren werden in Hongkong bei konstantem Bevölkerungswachstum
ca. 7.804.394 Menschen wohnen. |
Aufgabe 2)
| a) |
In Mexiko lebten 2008 ca. 103,3 Mio Einwohner. Gegenüber
dem Vorjahr waren dies Laut CIA World Factbook 1,142% mehr. Wie viele
Einwohner wird das Land bei gleichem Wachstum
in 10 Jahren haben?
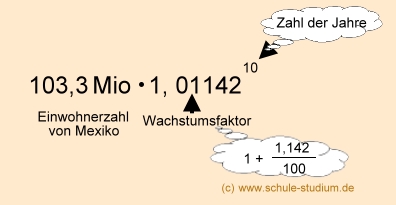
In 10 Jahren werden in Mexiko bei gleichem Wachstum ca. 115,7 Mio Einwohner
leben.
|
| b) |
Nach wie vielen Jahren wird Mexiko bei diesem Bevölkerungswachstum
110 Mio Einwohner haben?
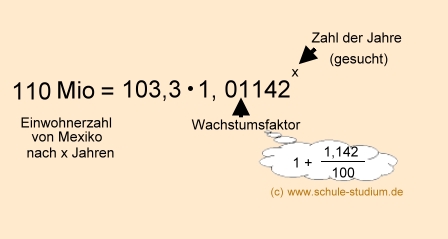

Antwort: Nach 5,5 Jahren wird Mexiko wohl bei gleichem Wachstum 110
Mio Einwohner haben. |
EXPONENTIELLER
VERFALL:
Aufgabe 3)
In einem See nimmt die Helligkeit pro Meter Wassertiefe um 18% ab. An der Oberfläche
beträgt die Helligkeit noch 100 LUX (Lichteinheit). Wie viele Lichteinheiten
sind es noch in 10 m Wassertiefe?
Lösung:
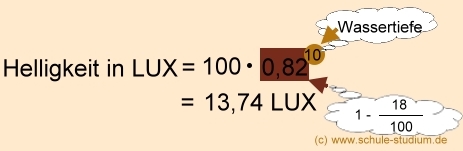
Antwort: In 10 m Wassertiefe sind nur noch 13,74 LUX zu messen.
|
Aufgabe 4)
Ein radioaktives Material zerfällt so, dass seine Menge stündlich um 9,2 % abnimmt.
Nach wie vielen ganzen Stunden ist erstmals weniger als 1/5 der Anfangsmenge
vorhanden?
Lösung:

Antwort: Nach 17 Stunden ist erstmals weniger als 1/5 der Anfangsmenge
vorhanden.
|
Aufgabe 5)
Bei 0°C Außentemperatur nimmt die Temperatur eines Heißgetränkes in
der Thermoskanne
stündlich um 14 % ab. Nach 4 Stunden werden in der Kanne 54 °C gemessen.
Wie heiß war das Getränk beim Einfüllen?
Lösung:

Antwort: Das Heißgetränk hatte beim Einfüllen eine Temperatur von 98,71
°C.
Aufgabe 6)
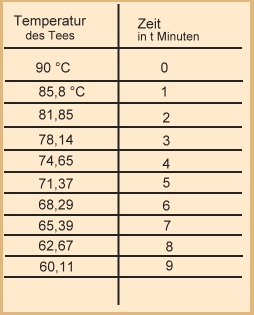
Eine Tasse Tee hat eine Temperatur von 90°C. Die Raumtemperatur beträgt 20°C.
Der Tee kühlt pro Minute um etwa 6%
der Differenz zwischen Raumtemperatur und der Temperatur des Tees ab. Nach t Minuten hat der Tee eine Temperatur
T = (20+ 70  0,94 t )°C. 0,94 t )°C.
Die Raumtemperatur soll als konstant angenommen werden.
Nach wie vielen Minuten hat der Tee eine Temperatur von 60°C?
Lösung:
zum besseren Verständnis ...
Der Wert 0,94 ergibt sich aus der 6%-igen Abkühlen des Tees pro Minute, sprich
1- 0,06 = 0,94.
Der Wert 70 aus obiger Gleichung ist die Differenz zwischen der Temperatur des Heißgetränks zu Beginn und der Raumtempertur (90°C - 20°C = 70°C)
60 = 20 + 70 0,94 t / -20 0,94 t / -20
40 = 70  0,94 t / 0,94 t /  70 70
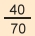 = 0,94 t = 0,94 t
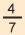 = 0,94 t = 0,94 t
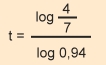
t = 9,04 min |
 |
|
|