|
|
Aufgabe:
Verwandle ein Rechteck in ein flächengleiches Quadrat.
Höhensatz des Euklid:
In jedem rechtwinkligen Dreieck hat das Höhenquadrat (h 2)
denselben
Flächeninhalt wie das Rechteck p * q.
 |
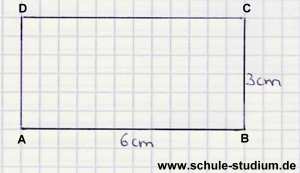Unser Rechteck, das wir nun in ein flächengleiches Quadrat
umwandeln wollen, ist 6 cm lang und 3 cm breit.
|
 |
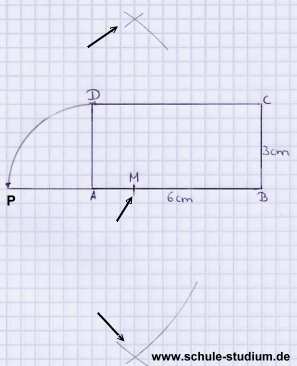Nun zeichnen wir den Mittelpunkt der Strecke PB ein.
(Siehe Geometrie: Mittelsenkrechte mit Zirkel einzeichen !)
|
 |
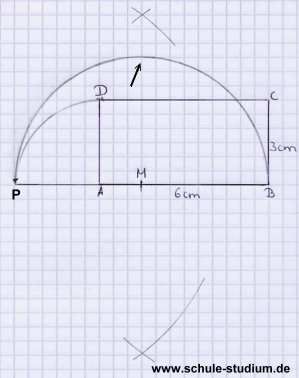Nun errichten wir auf der Strecke PB den Thaleskreis.
|
 |
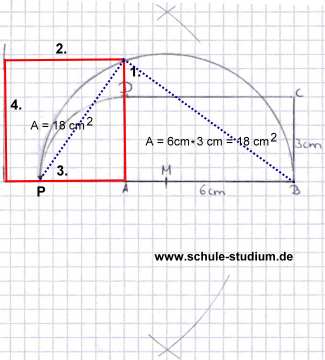Als Letztes verlängern wir die Strecke  über
D hinaus, so dass wir einen Schnittpunkt mit dem soeben errichteten
Thaleskreis erhalten.
Damit haben wir eine Seite des flächengleichen Quadrates
erhalten. Wir vervollständigen nun in einem letzten Schritt
das gesuchte Quadrat.
|
|
über A hinaus. Anschließend schlagen wir einen Viertelkreis
um A mit der Länge