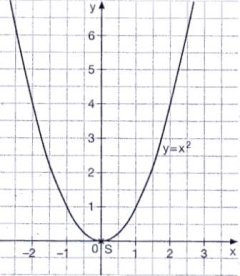
Der Graph der quadratischen Funktion f mit der Funktionsgleichung y=X² heißt Normalparabel.

Definitionsmenge D=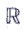
Wertemenge W = ⁺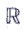

Hinweis:
Die Definitionsmenge ist die Menge aller X-Werte, welche die Funktion annnehmen kann.
Die Wertemenge ist dagegen die Menge aller Y-Werte, die der Graph annehmen kann. Wie wir dem Graphen entnehmen können, sind bei der Normalparabel nur positive Y-Werte möglich.

Im Scheitelpunkt S(0/0) der Normalparabel nimmt die Funktion f ihren kleinsten Funktionswert an.

Die Normalparabel ist nach oben geöffnet.

Der Graph der quadratischen Funktion f mit der Funktionsgleichung y = x² +2 ist eine nach oben verschobene Normalparabel.

Definitionsmenge D=
Wertemenge W = {Y /Y2}

Im Scheitelpunkt S(0/2) der Normalparabel nimmt die Funktion f ihren kleinsten Funktionswert an.

Die Normalparabel ist nach oben geöffnet.

Der Graph der quadratischen Funktion f mit der Funktionsgleichung y = x² -1 ist eine nach unten verschobene Normalparabel.

Definitionsmenge D=
Wertemenge W = {Y /Y-1}

Im Scheitelpunkt S(0/-1) der Normalparabel nimmt die Funktion f ihren kleinsten Funktionswert an.

Die Normalparabel ist nach oben geöffnet.

Der Graph der quadratischen Funktion f mit der Funktionsgleichung y = (x-1)² ist eine nach rechts verschobene Normalparabel.

Definitionsmenge D=
Wertemenge W = ⁺

Im Scheitelpunkt S(1/0) der Normalparabel nimmt die Funktion f ihren kleinsten Funktionswert an.

Die Normalparabel ist nach oben geöffnet.

Der Graph der quadratischen Funktion f mit der Funktionsgleichung y = (x+1)² ist eine nach links verschobene Normalparabel.

Definitionsmenge D=
Wertemenge W = ⁺

Im Scheitelpunkt S(-1/0) der Normalparabel nimmt die Funktion f ihren kleinsten Funktionswert an.

Die Normalparabel ist nach oben geöffnet.