Arithmetisches Mittel:

Man addiert die gegebenen Werte und teilt durch die Anzahl der Werte.

Bsp: 2, 4, 5, 2

arithmetisches Mittel:

  

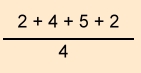Anwendungsbeispiel:

Eine Schülerin hat folgende mündliche Noten : 2-, 3+, 4, 2+.
Sie möchte nun wissen, wie sie in dem betroffenen Fach mündlich steht.
Ihr Lehrer meinte zu ihr, dass alle mündlichen Noten gleichermaßen zählen.






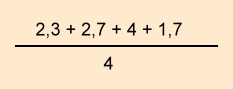
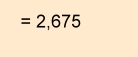
Die Schülerin steht in dem betroffenen Fach also auf 2,7 in mündlich.




Median:

Man sortiert zunächst die Werte ihrer Rangfolge nach. Der in der Mitte stehende
Wert ist dann der Median.

Bsp 1) ungerade Zahl von Werten:



2, 24, 5, 12, 4, 16, 7, 9, 25


Wir sortieren:

2

4

5

7

9

12

16

24

25

Der Median kann hier recht einfach und auch eindeutig bestimmt werden:
Median = 9, denn er ist der mittlerste der 9 Werte.

Der Median hat hier genau 4 Vorgänger (2,4,5, 7)
und 4 nachfolgende Werte (12,16,24,25).




Mittelwert:

Man ermittelt zunächst Klassen und teilt die Werte den jeweiligen Klassen zu. Anschließend wird durch die
Summe der Werte in den jeweiligen Klassen dividiert.

Bsp.:

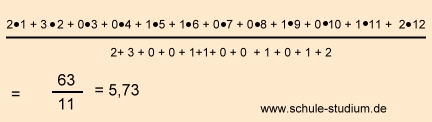
Es soll als Mittelwert erfasst werden, wann, d.h. in welchem Monat, die Schüler eines Kurses der
Abendschule Geburtstag haben.

Folgende Geburtstage ergeben sich:

13.1; 17.01; 09.02; 10.02, 01.02, 03.05, 07.09; 11.11, 17.06, 05.12, 20.12

Monat	1	2	3	4	5	6	7	8	9	10	11	12
Zahl der Schüler:	2	3	0	0	1	1	0	0	1	0	1	2

Boxplot:

Wir ordnen die Werte nach ihrer Rangfolge.
Anschließend ermitteln wir den Median bzw. den Median der oberen
und unteren Hälfte.