| Widerstand | Spannung | Stromstärke |
| R | U | I |
 |
Volt | Ampere |
Es gelten folgende physikalische Gesetze:
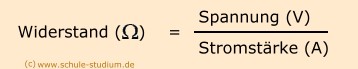
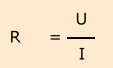
Gebräuchliche Einheiten für den Widerstand sind:
1 Ohm = 1
1 Kiloohm = 1000
1 Megaohm = 1000.000
Wandelt man obige Formel nach mathematischen Grundregeln um, so erhält man:
bzw. 
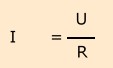
Ein elektrischer Leiter hat den Widerstand von 1
,
wenn durch ihn bei einer angelegten Spannung von 1 Volt ein Strom der Stärke
1 Ampere fließt. Das ohmsche Gesetz:
Um das ohmsche Gesetz besser zu verstehen,
sollten wir zunächst einen Blick auf folgende Messwerte-Tabelle werfen:
| Spannung U |
Stromstärke I |
Widerstand |
| 1 V | 0,5 A | 2 |
| 2 V | 1 A | 2 |
| 3 V | 1, 5 A | 2 |
| 4 V | 2 A | 2 |
| 5 V | 2,5 A | 2 |
| 6 V | 3 A | 2 |
An den Messwerten der Tabelle können wir unschwer erkennen, dass Spannung und Stromstärke bei konstantem Widerstand proportional zueinander sind, d.h. eine Verdoppelung der Spannung zieht auch eine Verdoppelung der Stromstärke mit sich. Verdreifacht sich die Spannung, so auch die Stromstärke.
Diese Abhängigkeit zwischen Spannung und Stromstärke bezeichnen wir als das OHMSCHE GESETZ !!
| OHMSCHE GESETZ: Spannung und Stromstärke sind einander direkt proportional.  Der Widerstand ist dabei konstant. |
Wichtig dabei:
Das ohmsche Gesetz gilt nur für metallische Leiter und für Kohle und nur bei konstanter Temperatur.
(also bei kleinen STrömen und bei Kühlung der Leiter.
Denn es gilt:
| Beziehung TEMPERATUR - WIDERSTAND: Je höher die Temperatur eines metallischen Leiters, desto größer ist sein Widerstand. Je niedriger die Temperatur ist, desto kleiner ist der Widerstand. |
Anwendung des ohmschen Gesetzes:
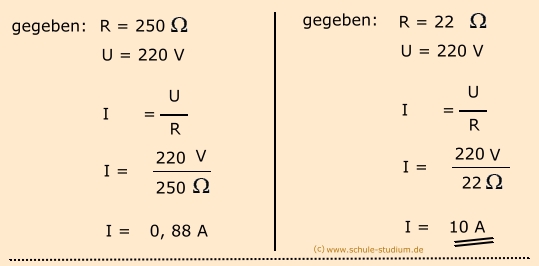
Frage: Wovon hängt der Widerstand eines Leiters ab? :
Der jeweilige Widerstand eines Leiters ist abhängig von 3 Größen
a) Material
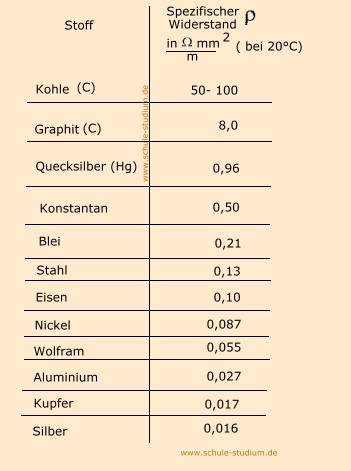
b) Länge
-> Der Widerstand R eines Leiters nimmt im gleichen Maße zu wie seine Länge vergrößert wird und umgekehrt.
c) Querschnittsfläche
-> Der Widerstand R verhält sich antiproportional zu der Querschnittsfläche(A), d.h. der
Widerstand R nimmt im gleichen Maße ab, wie man seine Querschnittsfläche S vergrößert.
Für den Widerstand R eines Materials mit der Länge l und der Querschnittsfläche A gilt:
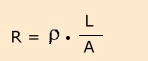
Die Wert
ist
abhängig vom Material (siehe obige Tabelle) 
Beispiel für de Berechnung des spezifischen Widerstandes:
