1 Torr = 1,333224·10²N/m²

1 N/m² = 1/100 000bar

1N/m² = 10µbar

1Torr = 1,33224·10³µbar

1Torr = 13,59510 kp/m²

1 Pa = 1 N/m² = 1/100 000 bar

1 bar = 100 kPa

1 bar = 10 N/cm²

1 mbar = 1cN/cm²

1 bar = 1,019716 at

1 at = 0,735559·10³ Torr

Aluminium 2,70 g/cm³

Blei 11,34 g/cm³

Eisen 7,86 g/cm³

Gold 19,3 g/cm³

Kupfer 8,93 g/cm³

Platin 21,4 g/cm³

Silber 10,1 g/cm³

0ºC = 0,06 m

5ºC = 0,09 m

10ºC = 0,12 m

20 ºC = 0,24 m

30ºC = 0,43 m

40ºC = 0,75 m

50ºC = 1,25 m

60ºC = 2,02 m

70ºC = 3,17 m

80ºC = 4,82 m

90ºC = 7,14 m

100ºC = 10,33 m

 

Physik - Aufgaben

 

1) Aufgabe für die Steighöhen in einem U-Rohr

Wie hoch steht das Wasser im rechten Schenkel eines U-Rohres über einem Quecksilberspiegel im linken Schenkel,

wenn die Wassersäule die Länge h₁ =20 cm hat?

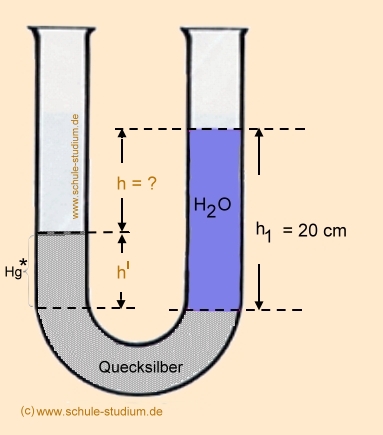
Lösung:
Die Wassersäule über dem Quecksilber auf der rechten Seite des U-Rohrs drückt auf der linken Seite die Quecksilbersäule hoch.
Das Gewicht der Wassersäule mit der Höhe h₁muss dem Gewicht der Quecksilbersäule mit der Höhe h' entsprechen.

G= r²·π·h'·ρ·g


Merke:
g = Ortsfaktor (in der Schule in der Regel mit 1 cN/g angegeben.

G_Wasser=G_Hg*

G_Wasser=r²·π·h₁•·ρ_W·g

G_Hg=r²·π·h'·ρ_Hg·g

r²·π·h₁ •·ρ_W·g=r²·π·h'·ρ_Hg·g

h'=h₁ •ρ_W /ρ_Hg

h' = 20•1/13,55

h' = 1,47 cm

Der linke Quecksilberspiegel ist ca. 1,47cm höher als der rechte Quecksilberspiegel.





Berechnung der Differenz zwischen Wasserspiegel und Quecksilberspiegel:

h_d = h₁-h'

h_d = 20-1,47

hd =18,53 cm

-> Somit ergibt sich eine Differenz zwischen Wasserspiegel und Quecksilberspiegel von 18,53 cm.

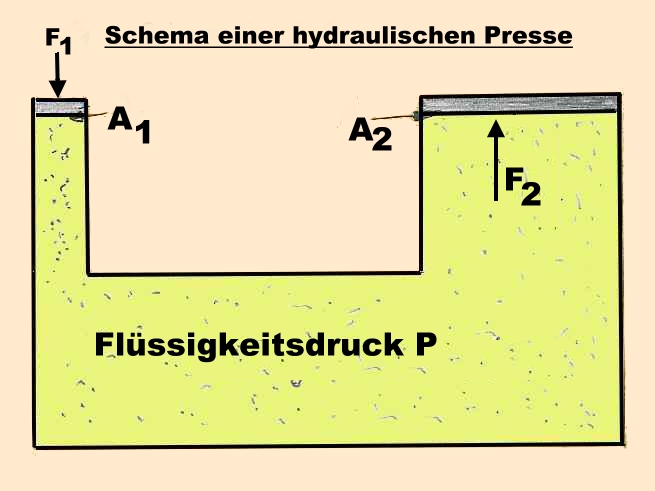
2) Aufgabe zur Anwendung des Kolbendruckes

Der kleine Kolben einer hydraulischen Presse hat 16 cm² Quersschnittsfläche. Wirkt auf ihn die Kraft 1600 N, erfährt der große Kolben die Kraft von 60 KN. Welcher Druck herrscht in der Fl&uumlssigkeit?. Welchen Querschnitt und welchen Durchmesser hat der zweite Kolben?

Formel: p = F : A

a) Berechnung des Druckes in der Flüssigkeit

p = 1600N : 16 cm²

p = 100N/cm²

b) Berechnung des Querschittes und des Durchmessers des 2. Kolbens.

A = F : p

A = 60000N : 100N/cm²

A = 600 cm²

c) Berechnung des Durchmesser des Kolbens

Formel: A = r²·π

r²= 600 : 3,14159265

r = 13,819766 cm

d = 2· 13,819

d =27,64 cm

3) Aufgabe zur Berechnung des Druckes auf eine Ausstiegsluke unter Wasser

Im Jahre 1953 tauchte Prof Piccard 3150 m tief. Mit welcher Kraft drückte
das Wasser auf die kreisförmige Ausstiegsluke. (Durchmesser 80 cm)

Druck in der Tiefe

p= 3150/10 bar

p= 315 bar

Druck auf den Deckel

p = 315 bar = 3150 N/cm²

Fläche(A) = r²·π

A = 40²·π

A = 5024 cm²

Zuhaltekraft auf dem Deckel

Formel: F = p·A

F =3150 N/cm²·5024 cm²

F = 15.825.600 N

4. Beispielaufgaben zur Berechnung des Auftriebes

Ein Körper wiegt in der Luft 90 cN, in Wasser 60 cN.
Berechne das Volumen des Körpers und seine Dichte; der Ortsfaktor g sei 1 cN/g

Berechne das Volumen des Körpers und seine Dichte!

Gewicht des Körpers in der Luft G_K = 90 cN

Gewicht des Körpers in Wasser = 60 cN

Scheinbarer Gewichtsverlust in Wasser = 30 cN

Gewicht der verdrängten Wassermenge nach dem Gesetz von Archimedes = 30 cN

Heimversuch: Oft ist es ja so, dass Versuche nicht Zuhause durchgeführt werden können. Aber gerade Versuche mit Phänomenen des Auftriebs können sehr gut in der heimischen Badewanne durchgeführt werden. Nimmt man zum Beispiel einen Luftballon mit in die Wanne und versucht diesen unter Wasser zu drücken gestaltet sich dies oft schon als schwierig. Den Druck nach oben merkt man auch, wenn man versucht einen Luftballon unter Wasser aufzublasen.

 

Berechnung des Volumens der verdrängten Wassermenge= Volumen des Körpers

Formel: V_Fl = G_Fl / roFl·g

V_Fl = 30 cN/1ρ_Fl ·1cN/g

V_Fl = 30 cm³

VFl=Vk= 30cm³

Berechnung der Masse

mK = GK/g

mK = 90/1cN/g

mK = 90g

Berechnung der Dichte des Körpers

ρK = mK/V

ρK = 90g/30cm³

ρK = 3g/cm³

 

5) Beispielaufgabe für die Berechnung des Volumens und der Gewichtskraft einens Körpers

Ein Körper aus Aluminium erfährt in Wasser einen scheinbaren Gewichtsverlust von 1 N.
Berechne Volumen und Gewichtskraft des Körpers!
Dichte des Aluminiums = 2,7g/cm³ Berechnung des Volumens

V = G/ρ·g

V = 100cN · g · cm³/1cN · 1g

V = 100cm³

Berechnung der Gewichtskraft

G = ρ·V·g

G = 2,7g·100 cm³·1 cN/cm³·g

G = 270 cN

 

6) Weiteres Beispiel für den Auftrieb

Aufgabenstellung: Ein rechteckiger Balken ist 6 m lang, 40 cm breit und 40 cm hoch. Er hat eine Dichte von 0,46g/cm³ 1.
Wie tief taucht der Balken ins Wasser ein? 2. Im Wasser wollen sich 10 Menschen an dem Balken festhalten,
um sich vor dem Ertrinken zu retten.

Jeder drückt ihn beim Festhalten mit 230 N ins Wasser.
Geht der Balken unter? Wenn nicht, wie hoch ragt er noch aus dem Wasser heraus?

Berechnung des Volumens des Balkens:

V_Balk = Länge·Breite·Höhe

V_Balk = 600cm·40cm·40cm

V_Balk = 960.00 cm³

Berechnung der Gewichtskraft des Balkens

G= ρ·V·g

G= 0,46g/cm³·960.000cm³·1cN/g

G=441600 cN

Durch die Menschen ausgeübte Kraft:

G_Mensch = 10·230N

G_Mensch = 2300 N

Beweis der Schwimmfähigkeit des Balkens bei voller Belastung

 

Berechnung des verdrängten Flüssigkeitsvolumens aufgrund des Gewichtes des Balkens

V = G/ρ·g

V= 441600·cm·g/1g·1cN

V = 441600cm³

Berechnung der Eintauchtiefe ohne Belastung

H = V/L·B

H = 441600cm³/600cm·40cm

H = 18,4cm

Berechnung der Eintauchtiefe des Balkens bei Belastung durch Balken und Mensch

V = L·B·H=G/ρ·g

H = G/ρ·g·L·B

H= 671600·cm³· g/1g · 1cN · 600cm³ · 40cm³

H=27,983333cm

Berechnung der Höhe des Balkens über Wasser


Höhe des Balkens = Gesamthöhe - Eintauchtiefe

H_{über Wasser} = 40cm - 27,98333 cm

H_{über Wasser} = ca. 12,02cm

Berechnung der Auftriebskraft des Balkens beim Eintauchen

V_Balk = 960000 cm³ wie berechnet

G_Wasser = 960000cm³ · 1g·1cN/cm³·g

G_wasser = 960000 cN

Gesamtkraft = G_Balk+G_Mensch

Gesamtkraft = 441600 cN + 230000 cN

Gesamtkraft =671600 cN

Schwimmbeweis = G_Wasser- G_Balk+Mensch

Schwimmbeweis = 960000 cN - 671600 cN

Schwimmbeweis = 288400 cN

Schlussfolgerung: Der Balken schwimmt noch.

 

7) Aufgabe über die Bestimmung der maximalen Saughöhe

Bestimme die maximale Saughöhe für Wasser von 50º bei einem Luftdruck von 726 Torr

p in N/m²= Druck in Torr·Umrechnungsfaktor

p = 726 · 133,3224 N/m²

h = p/ρ·g

h = 96792·N·kg·m³/m²·9,81N·10³·kg

h = 9,87 m

h_i bei 50 ºC aus obiger Dampfdrucktabelle = 1,25 m

Da der Dampfdruck der Flûssigkeit abzuziehen ist gilt:

h_max= h - h_i

h_max = 9,87m-1,25m

h_max = 8,62 m

Die maximale Saughöhe wäre somit 8,62 m.
Die wirkliche Saughöhe wäre jedoch aufgrund verschiedener Faktoren geringer.

© www.schule-studium.de

Die Verlagsplattform für den Fachbereich Englisch Unterrichtsmaterialien, Lernhilfen, Interpretationen, Lektüren Surftipp: Besuchen Sie doch auch folgende Webseiten: Eventportal   Englisch Lektüren Englisch Plattform Deutsch Plattform Mathe Plattform : : : : : www.parties-und-events.de www.english-readers.de www.englisch-unterrichtsmaterialien.de www.deutsch-unterrichtsmaterialien.de www.mathe-unterrichtsmaterial.de