Halbwertzeiten einzelner radioaktiver Substanzen
:
Schwefel (radioaktiv)
Halbwertzeit : 9 Jahre
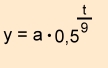
| t in Jahren |
radioaktives Material in g |
| 0 |
1 g |
| 1 |
0,926 |
| 2 |
0,857 |
| 3 |
0,794 |
| 4 |
0,735 |
| 5 |
0,680 |
| 9 |
0,500 |
| 10 |
0,463 |
| 20 |
0,214 |
| 40 |
0,0459 |
| 50 |
0,0213 |
| 100 |
0,00045 |
Plutonium 239
Halbwertzeit : 24 000
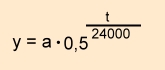
| t in Jahren |
radioaktives Material in g |
| 0 |
1 g |
| 1 |
0,9999 |
| 10 |
0,9997 |
| 100 |
0,997 |
| 1.000 |
0,971 |
| 5.000 |
0,866 |
| 10.000 |
0,749 |
| 24.000 |
0,500 |
| 50.000 |
0,236 |
| 100.000 |
0,0557 |
Aufgabe:
Nach wie vielen Jahren hat die Strahlung auf weniger als 1/°°
der ursprünglichen
Strahlung abgenommen?
Antwort:

Caesium 137
Halbwertzeit : 33 Jahre
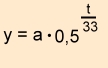
| t in Jahren |
radioaktives Material in g |
| 0 |
1 g |
| 1 |
0,979 |
| 10 |
0,811 |
| 33 |
0,5 |
| 50 |
0,350 |
| 100 |
0,122 |
| 200 |
0,015 |
| 300 |
0,002 |
| 400 |
0,00022 |
| 500 |
0,000027 |
Aufgabe:
Nach wie vielen Jahren sind von 2 Gramm radioaktivem Caesium 137
noch 1/100 übrig
?
Antwort:

Radium
Halbwertzeit : 1843 Jahre
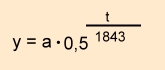
| t in Jahren |
radioaktives Material in g |
| 0 |
1 g |
| 1 |
0,9996 |
| 10 |
0,9962 |
| 100 |
0,9631 |
| 1.000 |
0,6865 |
| 1.843 |
0,5 |
| 5.000 |
0,1525 |
| 10.000 |
0,0233 |
| 15.000 |
0,003548 |
| 20.000 |
0,000541 |
Aufgabe:
Bei Radium ist nach 593 Jahren 20% der Augangsmasse zerfallen.
a) Wie lautet der Zerfallsfaktor?
-> 0,8
b) Nach wie vielen Jahren ist 99/100, d.h. 99% der Ausgangsmasse zerfallen?

Anwort:
Im 3940 Jahr ist 99% der Ausgangsmasse verfallen.
Oder anders ausgedrückt
...
noch
1% der ursprünglichen radioaktiven Masse von Radium vorhanden.
-> Musteraufgaben
zum Thema Logarithmus
-> Mathe Lernhilfen. Übungsaufgaben mit Lösungen |
|


Mathe Lernhilfen
zum Themenbereich
Logarithmen
& Exponentialgleichung
Mathe Lernhilfe
10. Klasse:
|
|
Komplett Trainer
Mathematik 10. Klasse
Gymnasium |
|
|
Wissen Üben Testen
Mathematik 10. Klasse
|
|
|
Abschlussprüfung
Mathematik 10. Klasse
Realschule |
|
|
Fit in Test und Klassenarbeit
Mathematik
10. Klasse
|
|
|
Mathematik 10. Klasse Realschule
Wahlpflicht-fächergruppe II/III
|
|
|
Mathematik 10. Klasse Bayern
Schulaufgaben
|
STARK LERNHILFEN
im Überblick
|
|