Lösen von Gleichungen 4. Grades, Wie löst man Gleichungen 4. Grades?

Berechnung von Funktionen 4. Grades

Im Folgenden sollen ein paar Beispielaufgaben 4. Grades gelöst werden:

Beispielaufgabe Nr. 1)

Hinweis:

Liegt eine Gleichung 4. Grades vor, die lediglich gerade Exponenten aufweist, so ist es möglich einfach auszuklammern.

Es gilt:
"EIN PRODUKT IST DANN NULL, WENN EINER DER FAKTOREN NULL IST."

Daraus folgt, dass entweder = 0 sein muss, oder aber - 4 + = 0.

Beispielaufgabe Nr. 2)

a = 1

b = - 13

c = - 48

;

1.	Zunächst müssen die beiden Klammern nach dem Distributivgesetz ausmultipliziert werden.

2.	Anschließend wird die Gleichung so umgestellt, dass rechts vom Gleichheitszeichen der Wert 0 steht.

3.	Nun wird = u gesetzt, um die Gleichung lösen zu können.

4.	Wir bestimmen nun die Variablen a, b und c und wenden die abc- Formel an. In diesem Fall wird die Diskriminante berechnet und anschließend u₁und u₂bestimmt.

5.	Da = u ist, müssen wir nun wieder nach X auflösen. Da man nicht die Wurzel einer negativen Zahl nehmen kann, kommt - 3 als Lösung nicht in Frage.

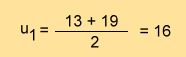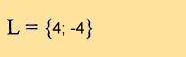=> weitere Lernhilfen

=> zurück zum Hauptmenu des Faches Mathematik

Berechnung von Funktionen 4. Grades