Zur Beantwortung dieser Frage, sollte man sich als Erstes noch einmal in
Erinnerung rufen, was der Kosinus eines Winkels

Da die Hypothenuse im Einheitskreis stets 1 ist, so entspricht der Cosinus des
Winkels
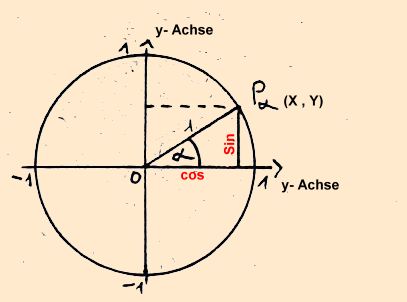
Ist
Den Wert ermitteln wir duch Ablesen des ´x´-Wertes auf dem Millimeter-Papier
(ca. 2,9 cm) nach Umrechnung im 3cm Einheitskreises!!!
(s. unten: Dreisatzrechnung)
Kosinus 15° im Einheitskreis dargestellt:

Da wir als Einheitskreis den Radius 3 cm gewählt haben, müssen wir,
um auf den exakten Wert zu kommen, folgendermaßen rechnen:
 |
 |
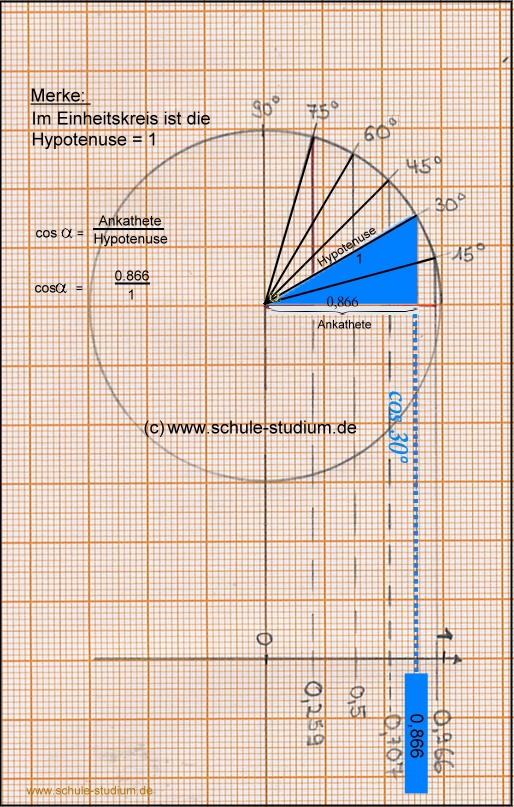
Kosinus 30° im Einheitskreis dargestellt:
Ist
ca. 0,866.(blaue Linie)
Den Wert ermitteln wir wieder durch Ablesen des ´x´-Wertes auf dem Millimeter-Papier
(hier: 2,6 cm) !!!
Eine Umrechnung mit Hilfe des Dreisatzes ergibt den Kosinuswert 0,867
(s. Dreisatzrechnung)

Dies entspricht dem exakten Wert:
gemäß Taschenrechner.
| Merke: cos 30° = |
Kosinus 45° im Einheitskreis dargestellt:

Ist
ca. 0,707. (Berechnung wie oben)
Exakter Wert:
Kosinus 60° im Einheitskreis dargestellt:

Tabelle der besonderen Kosinus Werte:
| 0° | 30° | 45° | 60° | 90° | |
| 1 | 0,5 | 0 |
Mathe Lernhilfen 9./10. Klasse zu den Themen Algebra und Geometrie Mathe Lernhilfe 10. Klasse:
Mathe Lernhilfe 10. Klasse:
Mathe Lernhilfe 9. Klasse:
Mathe Lernhilfe 9. Klasse:
Mathe Lernhilfe 9. Klasse:
Mathe Lernhilfe 10. Klasse:
Mathe Lernhilfe 10. Klasse:
Mathe Lernhilfe 10. Klasse:
Mathe Lernhilfe 10. Klasse:
Mathe Lernhilfe 10. Klasse:
Mathe Lernhilfe 10. Klasse:
Mathe Lernhilfe 10. Klasse:
Mathe Lernhilfe 10. Klasse:
Mathe Lernhilfe 10. Klasse:
|













