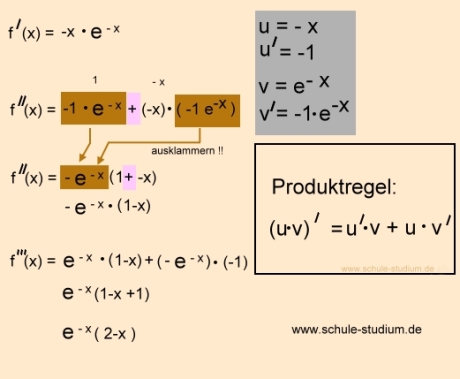
Aufgabe 2
Untersuchung auf Nullstellen :
Um die Nullstellen der Funktion zu bestimmen, setzen wir f(x) = 0
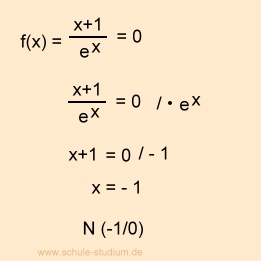
Prüfen auf eventuelle Extremwerte :
An einem Hoch- oder Tiefpunkt ist die Steigung der Funktion gleich Null. (siehe Graph)
Daher wird die erste Ableitung der Funktion f´(x) = 0 gesetzt.
 |
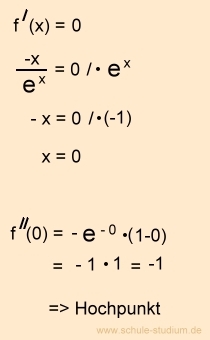In einem zweiten Schritt wird der gefundene Wert für x in die 2. Ableitung eingesetzt, um herauszufinden, ob es sich um einen Hoch- oder um einen Tiefpunkt handelt. Allgemein gilt: Ist  ein Wert > 0 so handelt es sich um einen TiefpunktIst ein Wert < 0 so handelt es sich um einen Hochpunkt. In diesem Beispiel ist = - 1, d.h. ein Wert kleiner als 0 und damit liegt bei x= 0 ein Hochpunkt vor. |
Wir zeichnen den Funktionsgraphen der e- Funktion:
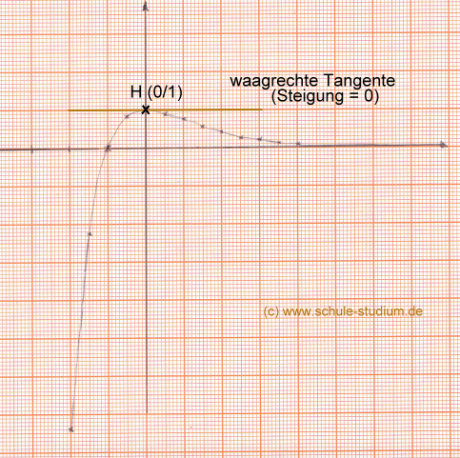
Grenzverhalten:
x ->
f(x) = 0Auch am Graphen ist leicht zu erkennen, dass bei y = 0 eine Asymptote liegt.
Weiterführende Verweise:
| -> | Fach
Mathematik des Schulportals |
-> | Mathematik Unterrichtsmaterial |
Mathe Unterricht: Mathe Übungsaufgaben mit Lösungen
weitere Lernhilfen > |
