Aufgabe 1
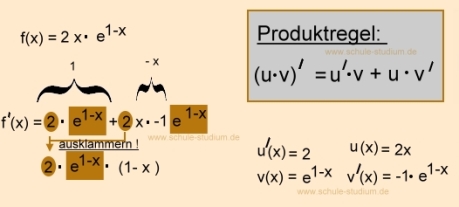

Untersuchung auf Nullstellen :

Prüfen auf eventuelle Extremwerte :
An einem Hoch- oder Tiefpunkt ist die Steigung der Funktion gleich Null.
(siehe Graph) Daher wird die erste Ableitung der Funktion f´(x) = 0 gesetzt.


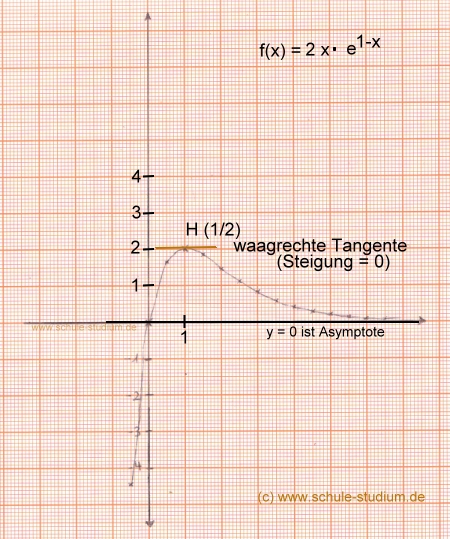
Wir zeichnen die Funktionsgraphen der e- Funktion:
Grenzverhalten:
x -> 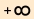 f(x) = 0 f(x) = 0
Auch am Graphen ist leicht zu erkennen, dass bei y = 0 eine Asymptote liegt.
Untersuchung auf Wendepunkte:
Ein Wendepunkt ist ein Punkt auf einem Funktionsgraphen, an welchem
der Graph sein Krümmungsverhalten ändert. Ein Graph wechselt hier
entweder von einer Rechts- in eine Linkskurve oder umgekehrt.
Um Wendepunkte zu berechnen wird 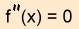 gesetzt. gesetzt.
Wir erhalten für x = 2. Da für 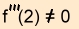 heraus kommt, ist in X =2 eine heraus kommt, ist in X =2 eine
Wendestelle.
Wendepunkt (2/ 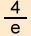 ) )
Weiterführende
Verweise:
|
|






![]() f(x) = 0
f(x) = 0![]() gesetzt.
gesetzt. ![]() heraus kommt, ist in X =2 eine
heraus kommt, ist in X =2 eine ![]() )
)







