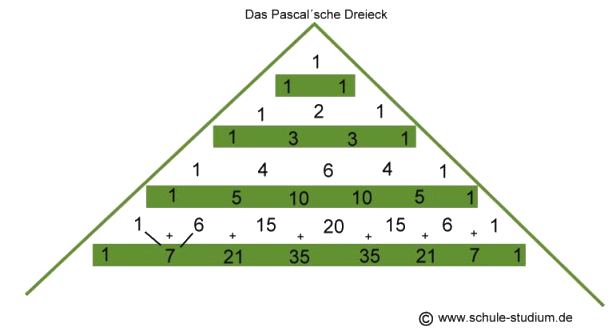
Das Pascal´sche Dreieck |
|
|
Anwendung
und Sinn des Pascal´schen Dreiecks: |
||
Das Pascal´sche Dreieck dient dazu, Rechenaufgaben vom Typ (a
+ b)x zu lösen, wobei X im
Allgmeinen größer
als 2 ist.
Vielen sind sicherlich die Binomischen Formeln geläufig....
1. Binomische Formel: (a + b)2 = a2 + 2 ab +
b2
2. Binomische Formel: (a - b)2 = a2 - 2 ab +
b2
3. Binomische Formel: (a + b)(a - b) = a2 - b2
Das Pascal´sche
Dreieck hilft nun bei Aufgaben
vom Typ (a + b)3, (a + b)4, (a + b)5....
Um den Nutzen des Pascal´schen Dreiecks zu demonstrieren, möchte
ich zunächst einmal auf herkömmliche Methode folgende Terme
berechnen:
(a + b)3 = (a + b)2 * (a + b) = ( a2 + 2 ab + b2) (a + b) = a3 + 2 a2b
+ ab2 + a2b + 2 ab2 + b3
= 1 a3 + 3a2b
+ 3 ab2 + 1 b3
| -> | Betrachten wir Zeile 3 des Pascal´schen Dreiecks,
so stellen wir eine perfekte Übereinstimmung der Koeffizienten
fest. : 1 3 3 1 interessant, oder???? |
(a + b)4 = (a + b)2 * (a + b)2 =
( a2 + 2 ab + b2) * ( a2 + 2 ab +
b2)=
a4 + 2 a3b + a2b2 + 2
a3b + 2 ab3 + a 2b2+ 2
a b3+ b4 =
1 a4 + 4 a3b
+ 6 a2b2 + 4 ab3 + 1 b4
| -> | Auch hier erkennen wir wieder eine faszinierende
Übereinstimmung mit den Koeffizienten des Pascal´schen Dreiecks: 1 4 6 4 1 faszinierend, oder???? |
Wir könnten diese Reihe noch weiter fortsetzen und ich glaube,
jedem ist klar, dass die Rechenarbeit immer größer würde
und immer mehr Zeilen benötigt würden, um Aufgaben wie (a
+ b)6 beispielsweise zu lösen. !?!?
Frage: Wie funktioniert nun das Pascal´sche Dreieck????
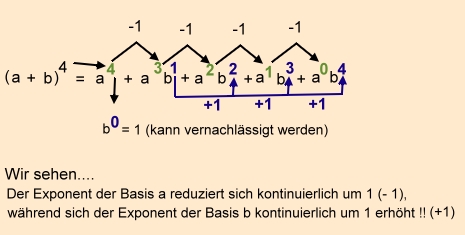
Damit lassen sich nun mit Leichtigkeit selbst Terme wie (a + b)8 mühelos berechnen. Probiert es selbst. Euer Webmaster.
weiterführende Links:
http://www.mpcx.net/mathe/pascalsche-dreieck.html
Mathe Lernhilfen zum Thema Terme + Binomische Formel Lernhilfen |
