Frage: Wie löse ich folgende Aufgaben zu
allgemeinen Sinus- und Kosinusfunktionen ??
1) Bestimme ohne Taschenrechner:
cos (x) =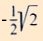
(-> siehe Tabelle M4)
 1
= 135°
1
= 135°
 2
= 225°
2
= 225°
 =
135° + k * 360° oder 225° + k * 360°
=
135° + k * 360° oder 225° + k * 360°
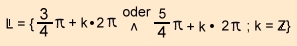
allgemeinen Sinus- und Kosinusfunktionen ??
1) Bestimme ohne Taschenrechner:
a) sin ( 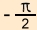 )
?? )
?? |
|
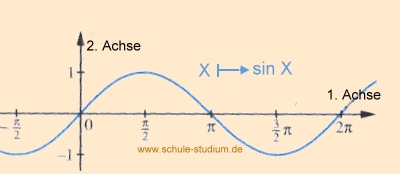
| Um die Aufgabe zu lösen, ist ein Blick auf die Sinuskurve sehr hilfreich. |
 |
|
An der Sinuskurve können wir leicht ablesen, dass der Sinus
von 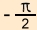 =
- 1 ist. =
- 1 ist. |
| b) sin ( |
|
| Um die Frage zu beantworten, müssen wir uns klar machen,
dass sich die Sinuskurve alle 2 Sprich sin ( |
| c) sin ( |
|
| Diese Aufgabe sieht auf den ersten Blick recht kompliziert
aus, ist sie aber nicht. Gemäß Tabelle M1 ist |
Winkelfunktion im Bogenmaß:
|
|||||||||||||||||||||||||
Tabelle der besonderen Sinus Werte:
|
d) cos ( 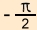 )
?? )
?? |
|
| Um die Aufgabe zu lösen, werfen wir wieder einen Blick auf die Cosinuskurve: |
Die Cosinuskurve: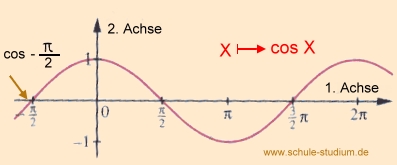 |
|
An der Cosinus-Kurve können wir leicht ablesen, dass der
cos von 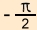 =
0 ist. =
0 ist. |
| e) cos ( - 5 |
|
| cos -5 |
Die Cosinuskurve im Bogenmaß: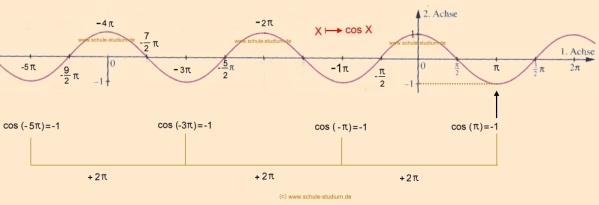 |
|
| An der erweiterten Cosinus-Kurve können wir leicht ablesen,
dass cos ( - 5 |
| e) cos ( |
|
| Auch hier wenden wir den gleichen Trick an. Wir addieren
2 |
Tabelle der besonderen Kosinus Werte:
|
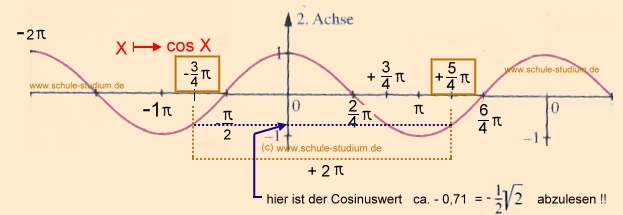 |
|||||||||||||||||||||||||||||||||||||||||||||
| An der Kosinus-Kurve können wir leicht ablesen, dass
gilt: cos ( SIN (x) und COS (x) im Überblick:
Tabelle M4 |
sin(x) = 0,5 (-> siehe Tabelle M4) 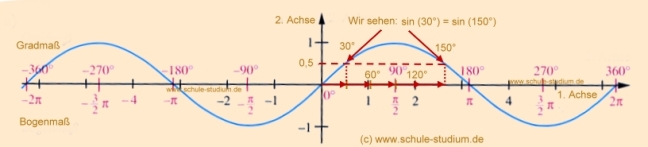 |
|
| sin(x) = (-> siehe Tabelle M4) 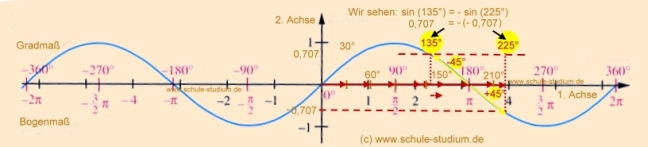 Es gilt für 0 sin Sprich wie rechnen wir?? sin 135 ° = - sin (360°-135°) = - (sin 225°) |
|
sin(x) = (-> siehe Tabelle M4) 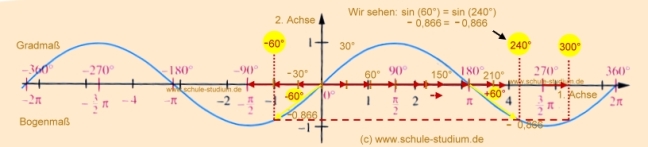 |
cos (x) =
(-> siehe Tabelle M4)













