Aufgabe :
Gegeben sind die Ebenen E mit A(3/2-1), B (6/0/5), C (-2/7/2)
sowie die Ebene
F mit K ( 4/1/9), L (-6/2/-9) und M ( 5/-1/-1).
Berechnung
des Normalenvektors:
Aus der Normalengleichung können wir sofort auch die Koordinatengleichung
aufstellen.
Die Koordinatengleichung der Ebene lautet
:
-36 X1 -39 X2 + 5 X3 = -191 |
| b) |
- > Ebene F |
| |
- > Ebene F, Normalenvektor berechnen ...

Auch bei Ebene F sollte man noch auf Orthogonalität prüfen:

Berechnung von d :
-> für Ebene F:
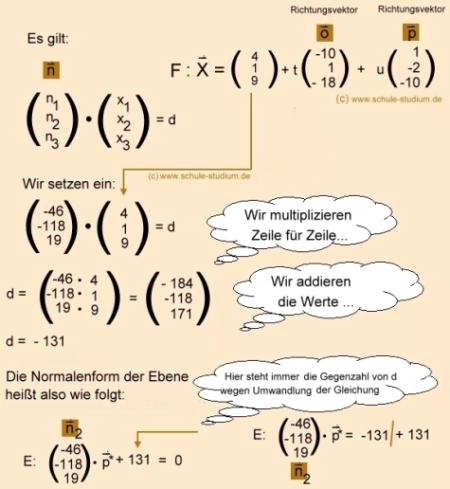
|
Aus der Normalengleichung können wir sofort auch die Koordinatengleichung
aufstellen.
Die Koordinatengleichung der Ebene lautet
:
-46 X1 -118 X2 + 19 X3 = -131 |
Mathe
Abi Lernhilfen:
(thematisch sortiert ...)
|
|