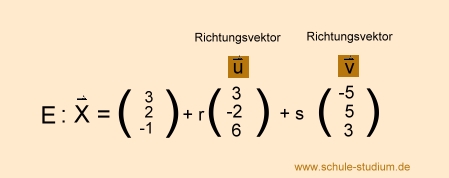
Frage: Wie berechne ich den Schnittwinkel zweier Ebenen ?
Aufgabe :
Gegeben sind die Ebenen E mit A(3/2-1), B (6/0/5), C (-2/7/2)
sowie die Ebene
F mit K ( 4/1/9), L (-6/2/-9) und M ( 5/-1/-1).
Berechne den Schnittwinkel beider Ebenen !!
Lösung:
1. Schritt:
Aufstellen der Parametergleichungen
beider Ebenen
EBENE E
mit A(3/2/-1), B (6/0/5), C (-2/7/2) :
Beim Ermitteln der Parametergleichung einer Ebene bleibt der Ortsvektor
unverändert.

EBENE F
mit K ( 4/1/9), L (-6/2/-9) und M ( 5/-1/-1).

Es handelt sich also um eine zwei durch die Richtungsvektoren 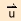 und und
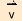 bzw. bzw.
 und und  aufgespannte Ebenen im dreidimensionalen Raum aufgespannte Ebenen im dreidimensionalen Raum
(ausgehend
vom angegebenen Ortsvektor)
.
2.
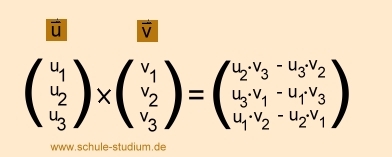
Schritt: Berechnung des Normalenvektors:
Im 2. Schritt muss der Normalenvektor beider Ebenen berechnet werden.
| b) |
- > Ebene F |
| |

- > Ebene F, Normalenvektor berechnen ...

Auch hier, bei Ebene F, sollte man noch auf Orthogonalität prüfen:

|
3.
Schritt: Berechnung des Schnittwinkels beider Ebenen:
Schneiden sich zwei Ebenen E und F, so gilt für ihren Schnittwinkel 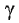 : :
 
Wie berechnen wir den Schnittwinkel aber?

Mathe
Abi Lernhilfen:
(thematisch sortiert ...)
|
|


![]() und
und
![]() bzw.
bzw.![]() und
und ![]() aufgespannte Ebenen im dreidimensionalen Raum
aufgespannte Ebenen im dreidimensionalen Raum![]() :
: