Lineare Funktionen Teil 4). Berechnung des Schnittpunktes zweier Geraden

Die allgemeine Darstellung linearer Funktionen lautet: f (x) = mx + t

Aufgabe 5) Ermittlung des Schnittpunktes zweier Geraden

gegeben sind folgende Funktionsgleichungen:

I) y = 6/5 x - 5,5
II) y = -0,5 x + 3

Frage: In welchem Punkt schneiden sich die beiden Geraden?

Bei Betrachtung der Funktionsgleichungen fällt auf, dass die erste Gleichung (I)
bei -5,5 den Schnittpunkt mit der y- Achse hat und eine positive Steigung aufweist

... und dass die zweite Funktion bei (0/3) den Schnittpunkt mit der y- Achse hat
und der Graph fällt (negative Steigung).

Wir zeichnen zunächst die Funktionsgraphen ...

(I) y = 6/5 x - 5,5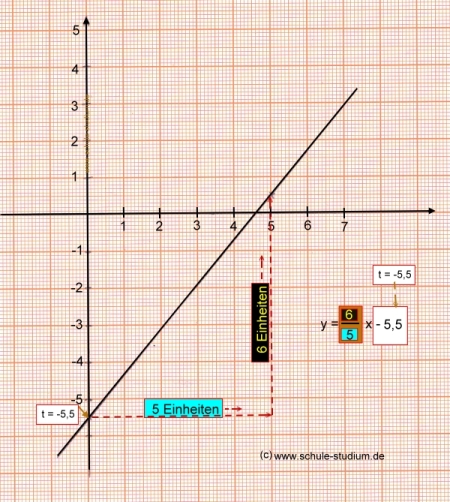

Lineare Funktionen - Bestimmung des Schnittpunktes

II) y = -0,5 x + 3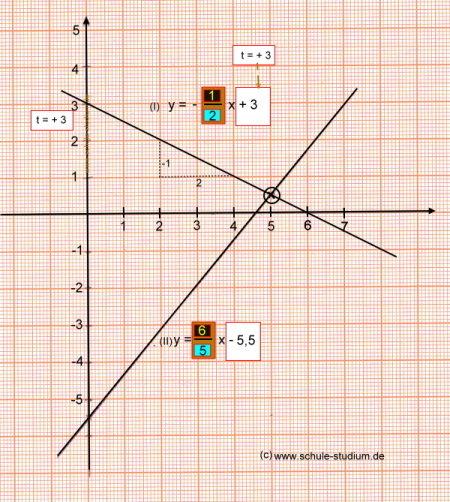

Lineare Funktionen - Bestimmung des Schnittpunktes

Am Graphen können wir bereits ablesen, dass sich die beiden Geraden im Punkt (5/0,5 )
schneiden.

Dies, d.h. den Schnittpunkt der Geraden möchten wir im Folgenden berechnen.

Um den Schnittpunkt zweier Geraden zu berechnen setzten wir die beiden
Funktionsgleichungen gleich.

Lineare Funktionen - Bestimmung des Schnittpunktes

Somit wissen wir schon mal den x- Wert des Schnittpunktes.

Zu berechnen ist nun der y- Wert, denn jeder Punkt hat schließlich einen x- und einen y- Wert.
Der y- Wert des Schnittpunktes kann durch Einsetzten des x- Wertes sowohl in Gleichung (I) als
auch in Gleichung (II) errechnet werden.

		Graphische Darstellung Linearer Funktionen (y = mx + t) m = Steigung, t= Achsenabschnitt auf der y- Achse (Teil 1)
		Graphische Darstellung Lineare Funktionen Berechnung des x-/y- Wertes und der Steigung m (Teil 2)
		Übung: Bestimmen der Funktionsgleichung durch Ablesen am Graph(Teil 3)
		Aufstellen einer linearen Funktionsgleichung bei nur zwei gegebenen Punkten (Teil 5)