| Untersuchung auf Symmetrie Punktsymmetrie/Achsensymmetrie |
11.Schuljahr (Oberstufe Gymnasium, Abitur)

11.Schuljahr (Oberstufe Gymnasium, Abitur) |
 |
| Übungen (Teil 4): Symmetrische Funktionsgraphen, aber keine Punktsymmetrie zum Ursprung - oder Achsensymmetrie zur y- Achse Wir untersuchen nun die folgenden Funktionen auf Symmetrie:
Hier handelt es sich um eine Normalparabel, die um 3 Einheiten nach rechts und eine Einheit nach oben verschoben ist. Außerdem ist sie nach unten geöffnet. Da achsensymmetrie wegen der geraden Potenz zu vermuten ist, prüfen wir diese mit dem uns bekannten allgemeinen Verfahren. Es muss also gelten f(x) = f(-x). Lösung:  Dennoch liegt eine Achsensymmetrie, wenn auch nicht zur y - Achse nahe. Daher zeichnen wir den Funktionsgraphen. 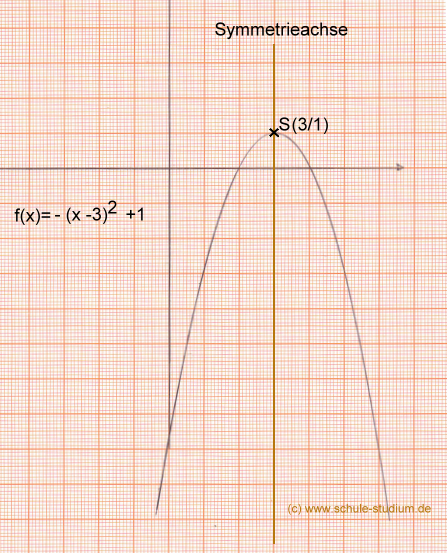
Da die ganzrationale Funktion sowohl ungerade (x3, X1) als auch gerade Hochzahlen (x0) hat, ist eine Punktsymmetrie zum Ursprung auszuschließen. Dennoch ist eine Punktsymmetrie wahrscheinlich. Wir prüfen also mit dem allgemeinen Verfahren, ob gilt f(-x) = - f(x).  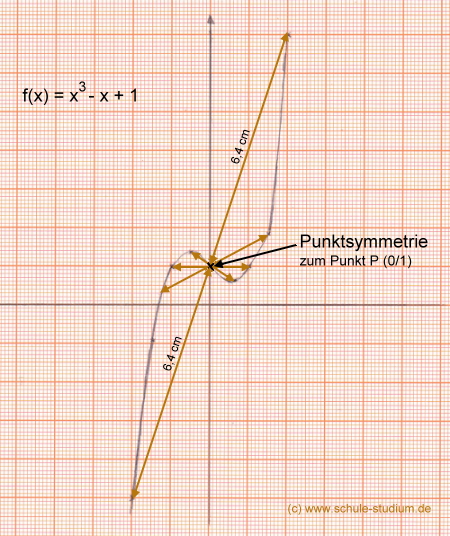 > Symmetrische Funktionsgraphen (Teil 2) > Symmetrische Funktionsgraphen (Teil 3) > Symmetrische Funktionsgraphen (Teil 4) Weiterführende Links:
|
|
|
|||||||||
| Die Schul- und Verlagsplattform für das Schulwesen Unterrichtsmaterialien (Kopiervorlagen, Stundenblätter, Arbeitsmittel, u.vm.) Surftipp: Besuchen Sie doch auch folgende Webseiten:
|
|||||||||