| Untersuchung auf Symmetrie Punktsymmetrie/Achsensymmetrie |
11.Schuljahr (Oberstufe Gymnasium, Abitur)

11.Schuljahr (Oberstufe Gymnasium, Abitur) |
 |
| Übungen (Teil 3): Wie bereits gesagt, kann man bei ganzrationalen Funktionen das Symmetrieverhalten anhand der Potenzen von x ablesen. Sind weder alle Potenzen von x gerade, noch ungerade - gilt also keiner der beiden Fälle - so heißt dies nur, dass keine Symmetrie bezügich der y- Achse bzw. des Ursprungs vorliegt. Es könnte durchaus aber eine andere Symmetrie vorliegen z.B. bezüglich einer anderen Achse oder aber eines anderen Punktes. Liegt keine ganzrationale Funktion vor, so muss das allgemeine Verfahren zur Ermittlung von Symmetrie angewendet werden: Bei Achsensymmetrie zur y- Achse muss gelten: f(x) = f(-x) Bei Punktsymmetrie muss gelten : f(-x) = - f(x) Wir untersuchen nun die folgenden Funktionen auf Symmetrie:
Da wegen des geraden Exponenten eine Achsensymmetrie zur y- Achse zu vermuten ist, prüfen wir nach dem allgemeinen Verfahren ob gilt: f(x) = f(-x). Lösung: 
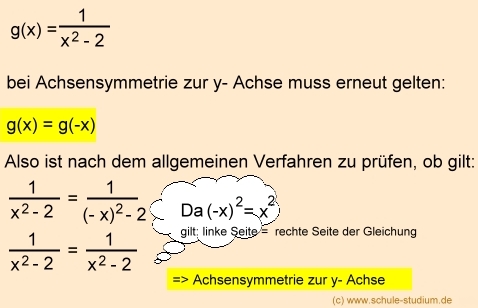
Da wir sowohl Achsensymmetrie zur y- Achse als auch Punktsymmetrie zum Ursprung (0/0) auf den ersten Blick nicht ausschließen können, prüfen wir nach dem allgemeinen Verfahren zunächst auf Achsensymmetrie, dann auf Punktymmetrie.  Wir untersuchen die Funktion auf Punktsymmetrie:  Zur Sicherheit zeichnen wir den Funktionsgraphen: 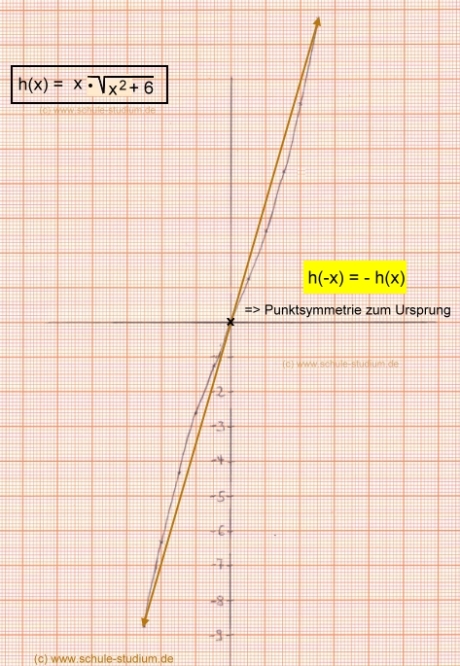 > Symmetrische Funktionsgraphen (Teil 2) > Symmetrische Funktionsgraphen (Teil 3) > Symmetrische Funktionsgraphen (Teil 4) Weiterführende Links:
|
|
|
|||||||||
© www.schule-studium.de > Unterrichtsmaterial > Mathe Unterricht Themenauswahl > Mathe Stationenlernen > Mathe Klausuren Oberstufe, mit Lösungen |
Die Schul- und Verlagsplattform für das Schulwesen Mathe Lehrer Unterrichtsmaterial (Mathe Kopiervorlagen, Mathe Arbeitsblätter, Stundenblätter, fertige Unterrichtsstunden für den Mathematikunterricht, Mathe Arbeitsmittel, Mathe Lernhilfen, Mathematik Übungsaufgaben mit Lösungen u.v.m.) Surftipp: Besuchen Sie doch auch folgende Webseiten:
|
||||||||