Lineare Gleichungssysteme

Frage:
Wie löse ich Textaufgaben
mit linearen Gleichungssystemen ??

-> Hühnchen & Bier

Aufgabe 1)
Räuber und Piraten nehmen an einem großen Gelage teil. Jeder der anwesenden Räuber isst 4 Hühnchen und trinkt 5 Bier. Ein Pirat dagegen isst nur 3 Hühnchen, dafür aber 7 Bier.

Zusammen werden bei dem großen Mahl 65 Hühnchen gegessen und 117 Bier getrunken.

Es ist zu errechnen, wie viele Räuber und Piraten an dem Gelage teilgenommen haben.




a) EINSETZUNGSVERFAHREN

Lösung der Aufgabe mit dem Einsetzungsverfahren.

Bei dem Einsetzungsverfahren wird die Gleichung zunächst nach einer Variablen
umgestellt. Dabei ist es dem Schüler überlassen, welche der gegebenen Gleichungen
er für die Umwandlung verwenden möchte und nach welcher Variablen er umformt.








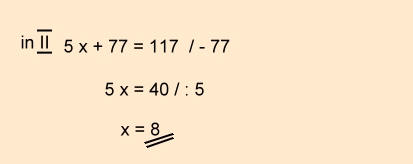
b) GLEICHSETZUNGSVERFAHREN
Textaufgabe: Hühnchen & Bier

Lösung der Aufgabe mit dem Gleichsetzungsverfahren.

Bei dem Gleichsetzungsverfahren müssen beide Gleichungen zunächst so umgeformt
werden, dass auf der linken Seite Gleichheit herrscht. Durch diesen Trick wird eine Variable
geschickt entfernt. Erst dann kann gleich gesetzt werden.







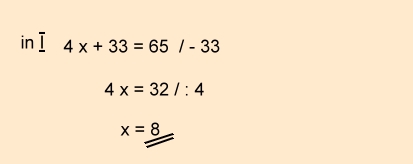
c) ADDITIONSVERFAHREN
Textaufgabe: Hühnchen & Bier

Lösung der Aufgabe mit dem ADDITIONSVERFAHREN

Bei dem Additionsverfahren müssen die beiden Ausgangsgleichungen zunächst
so umgefort werden, dass eine Variabel wegfällt. Da es sich im 2. Schritt um eine
Addition handelt, muss der Faktor der wegfallenden Variabel im Betrag identisch
und in der einen Gleichung positiv, in der anderen Gleichung negativ sein.

Weitere Aufgaben:

-> Lineare Gleichungssysteme als Textaufgabe
    (Piraten & Räuber: Bier und Hühnchen)

-> Lineare Gleichungssysteme als Textaufgabe
    (Hennen und Hasen: Beine im Tierstall)

     (nach 3 Lösungsverfahren gelöst: Einsetzungsverfahren,
     Gleichsetzungsverfahren, Additionsverfahren)  

- > Gleichungssystem mit 2 Variablen

(Tierbeine - Hennen + Hasen)

- > Gleichungssysteme mit 3 Variablen (Bsp. 2)

- > Gleichungssysteme mit 3 Variablen (Bsp. 3)

- > Gleichungssysteme mit 3 Variablen (Bsp. 4)

- > Gleichungssysteme mit 4 Variablen (Bsp. 5)

- > Gleichungssysteme in Matrizenform

(mit 4 Variablen

© www.schule-studium.de

Mathe Lernhilfen* 9./10. Klasse zu den Themen Algebra/Geometrie Mathe Lernhilfen Terme und Gleichungen Stark Klassenarbeiten Geometrie Mathematik Training Übungsaufgaben mit Lösungen, 9. Schuljahr Wiederholung Algebra Mathematik Training 9. Schuljahr Mathematik Training 9. Schuljahr Algebra und Stochastik 9. Schuljahr Mathematik Aufgaben mit ausführlichen Lösungen Mathe Lernhilfe 9. Klasse: Mathematik Klassenarbeiten Übungsaufgaben mit Lösungen, 9. Schuljahr Schulaufgaben Mathematik 9. Schuljahr Mathe Lernhilfe 9. Klasse: Mathematik KomplettTrainer Übungsaufgaben mit Lösungen, 9. Schuljahr Mathematik Training Übungsaufgaben mit Lösungen, 9. Schuljahr Lernplus Mathematik 9./10. Schuljahr Mathe Lernhilfe 5. - 10. Klasse: Mathematik Basiswissen 5.-10. Schuljahr -> weitere Lernhilfen -> Themenauswahl -> Unterrichtsmaterial     (Cornelsen) ->  Fach Mathematik des Schulportals