Wie funktioniert die quadratische Ergänzung und wozu dient sie?
Die quadratische Ergänzung dient dazu, eine Funktion 2. Grades in die Scheitelform zu bringen, so dass diese mit Hilfe der Verschiebungsregeln
und des ermittelten Scheitelpunktes gezeichnet werden kann. |
 |
5. Beispiel: Anwendung der quadratischen Ergänzung:
|
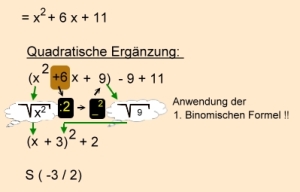
QUADRATISCHE ERGÄNZUNG
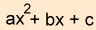
-> s. auch Kapitel Binomische Formeln
-> s. auch Kapitel Verschiebungsregeln
|
Merke:
Im ersten Schritt wird der
Summand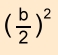
ergänzt, so dass im zweiten
Schritt mit Hilfe der 1. Binomischen Formelein Quadrat
(x +3)2 gebildet werden kann.
Bei dieser Aufgabe wird der
Wert 9 zunächst addiert, um
das 1. Binom aufstellen zu können.
Anschließend muss dieser Wert
wieder subtrahiert werden, um
das Ergebnis des Terms nicht zu verfälschen. |
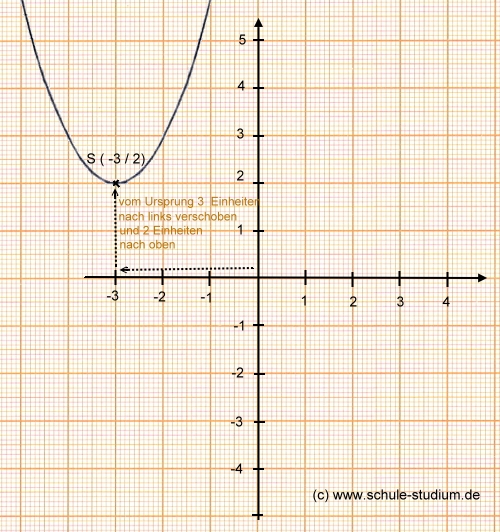
Die Funktion 2. Grades gezeichnet (Parabel):
(um 3 Einheiten nach links und um 2 Einheiten nach oben verschoben
6. Beispiel: Anwendung der quadratischen Ergänzung:
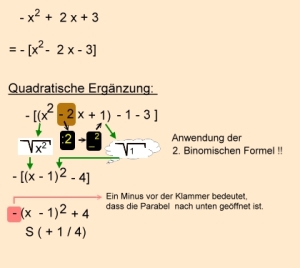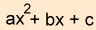
Um die quadratische Ergänzung verwenden zu können, muss der Wert a der allgemeinen Funktion gleich 1 sein (a = 1). |
Hier ist der Wert von a jedoch - 1. (a = -1)
Insofern muss - 1 ausgeklammert werden.
Erst dann kann mit der quadratischen Funktion begonnen werden. Bei dieser Aufgabe wird der Wert 1 zunächst addiert, um das 2. Binom aufstellen zu können.
Anschließend muss dieser Wert
wieder subtrahiert werden, um das Ergebnis des Terms nicht zu verfälschen. |
|
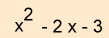
Um die Nullstellen der Funktion zu
ermitteln, empfielt es sich zunächst die
abc- Formel/Mitternachtsformel zu verwenden.
(s. links)
 |
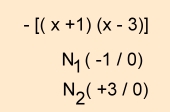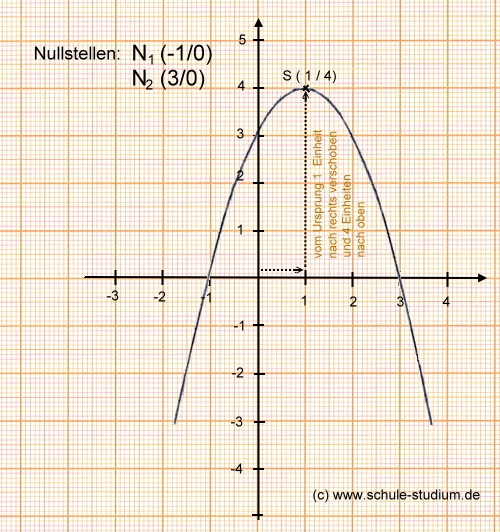
Die gezeichnete Funktion:
( um 1 Einheiten nach rechts und um 4 Einheiten nach oben verschoben,
| x |
-3 |
-2,5 |
-2 |
-1,5 |
-1 |
-0,5 |
0 |
0,5 |
1 |
1,5 |
2 |
2,5 |
3 |
3,5 |
4 |
| y |
-12 |
-8,25 |
-5 |
-2,25 |
0 |
1,75 |
3 |
3,75 |
4 |
3,75 |
3 |
1,75 |
0 |
-2,25 |
-5 |
-> Quadratische Ergänzung, (Teil 1)
-> Quadratische Ergänzung, (Teil 2)
-> Quadratische Ergänzung, hoher Schwierigkeitsgrad (Teil 4)
Weiterführende
Links:
|
| Mathe Unterricht:
zu den Themen der
9./10. Klasse
Lernhilfen
|
|
