1. Aufgabe:
Bestimme den zweiten Winkel :
Aufgabe 1a) sin  =
- sin 25°
es gilt:
I ) sin ( 180° - )
= sin
II) sin ( 180° + )
= - sin
III) sin (360° - =)
= - sin
Wir suchen also zwei Winkel bei denen Sinus negativ ist.
(wegen  sin 25°)
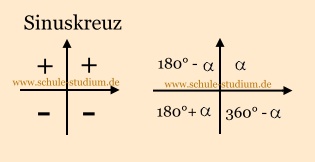
Bei Betrachtung des Sinuskreuzes erkennen wir sehr leicht, dass dies
im 3. und
4. Quadranten der Fall ist.
Folglich können wir die passenden Winkel wie folgt berechnen:
-> 180° +
=
205°
-> 360° - =
335°
Aufgabe 1b)
cos =
- cos 80°
es gilt:
I ) cos ( 180° - )
= - cos
II) cos ( 180° + )
= - cos
III) cos (360° - =)
= cos
Wir suchen also zwei Winkel bei denen Kosinus negativ ist. (wegen cos
80 °)
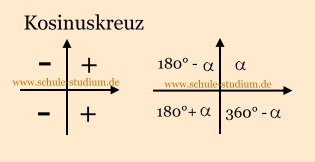
Bei Betrachtung des Kosinuskreuzes erkennen wir sehr leicht,
dass dies im 2.
und
3. Quadranten der Fall ist.
Folglich können wir die passenden Winkel wie folgt berechnen:
-> 180° - =
100°
-> 180° + =
260°
2. Aufgabe:
In welchen beiden Quadranten
liegt
jeweils
der Punkt P (cos/sin)
für den gilt:
Aufgabe 2a)
cos > 0
Lösung:
cos > 0
-> im 1. und 4. Quadranten
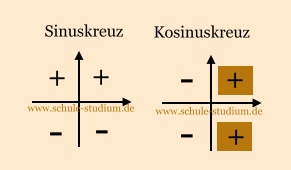
Aufgabe 2b)
sin > 0
Lösung:
sin > 0
-> im 1. und 2. Quadranten
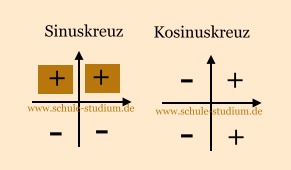
Aufgabe 2c)
sin  cos > 0
Lösung:
Wir erinnern uns an das bereits zurückliegende Kapitel der Mathematik
"Rechnen mit rationalen Zahlen" :
 ( )
=
( )
=
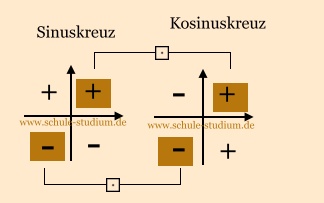
Folglich ist die Bedingung sin cos > 0
im 1 und 3. Quadranten erfüllt.
3. Aufgabe Gib den Quadranten und
jeweils zwei Winkel an für die Folgendes gilt:
Aufgabe 3a)
sin > 0
und cos < 0
Lösung:
sin > 0
-> im 1. und 2. Quadranten
cos < 0
-> im 2. und 3. Quadranten
Folglich ist obige Bedinung nur im 2. Quadranten erfüllt.
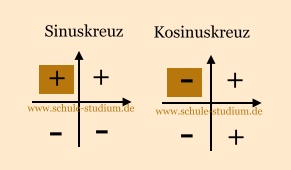
Aufgabe 3b)
sin < 0
und cos > 0
Lösung:
sin < 0
-> im 3. und 4. Quadranten
cos > 0
-> im 1. und 4. Quadranten
Folglich ist obige Bedingung nur im 4. Quadranten erfüllt.
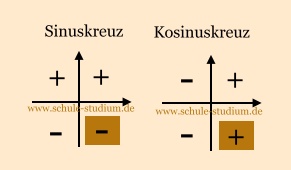
-> Sinus im Einheitskreis.
Hintergrundwissen
-> Sinus im
Einheitskreis. Grundlagen und Übungen
-> Kosinus
im Einheitskreis. Grundlagen und Übungen
-> Sinus- und Kosinusfunktionen.
Grundlagen und Übungen
|
