Frage:
Welche Arten von Geraden gibt es?(Klassifizierung von Geraden)
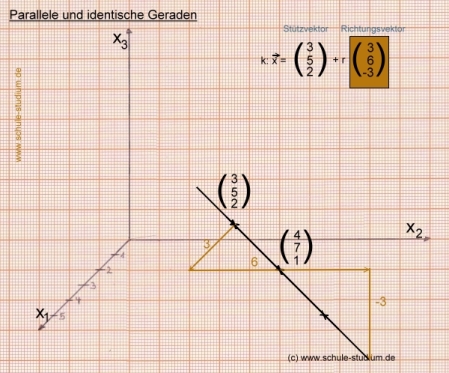
1. Parallele und identische Geraden
Behauptung: Folgende Geraden sind parallel und identisch:
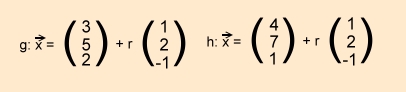
Woran erkenne ich nun, ob zwei Geraden parallel sind?
Antwort:
Haben zwei Geraden denselben Richtungsvektor, so sind diese parallel.
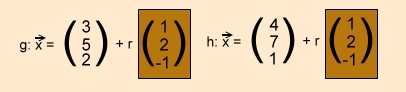
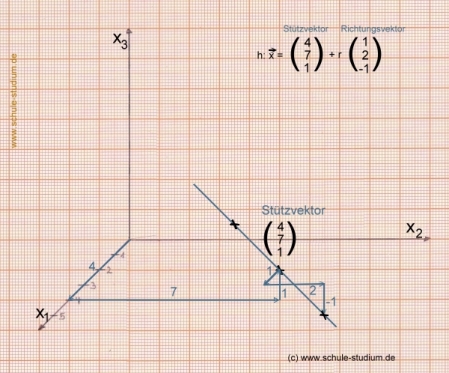
Nun ist aber noch zu klären, ob die Gerade g:x zu der Geraden h:x
parallel und verschieden (echt parallel) ist oder identisch.
Es gilt:
Liegt der Stützvektor der einen Gerade auf der parallelen Gerade, so
sind die Geraden parallel und zugleich identisch.
Um dies herauszufinden, ist eine Punktprobe notwendig.
PUNKTPROBE BEI EINER GERADEN:
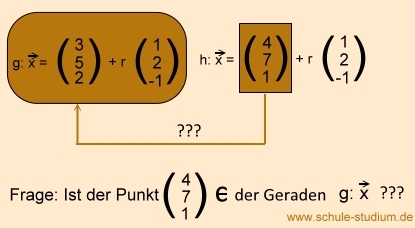

Da es ein ´r´gibt, dass alle 3 Gleichungen erfüllt, können wir davon ausgehen,
dass der Stützvektor der Geraden h:x auf der Geraden g:x liegt.
Folglich sind die beiden Geraden parallel und identisch.
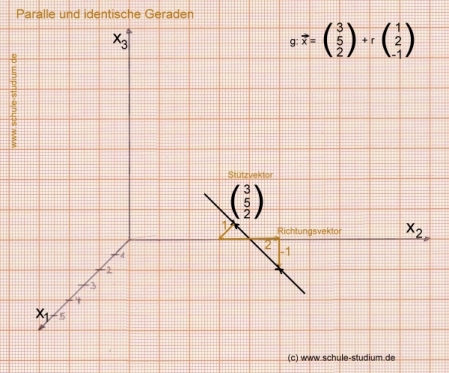
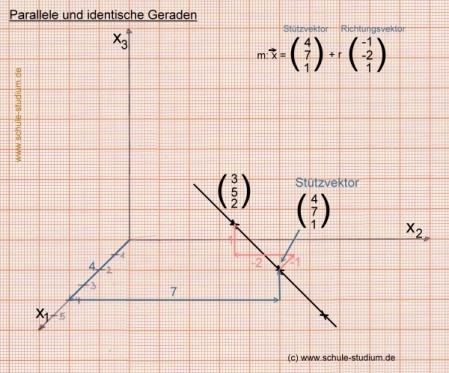
Parallel sind die Geraden aber auch, wenn der Richtungsvektor der einen Gerade ein
Vielfaches des Richtungsvektors der anderen Gerade ist.
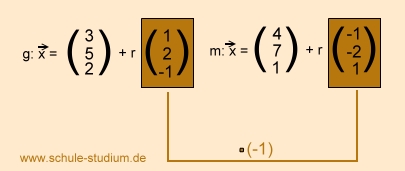
Bsp. 1)
Punktprobe erfüllt, Richtungsvektor der Geraden g:x
Vielfaches des Richtungsvektors von m:x
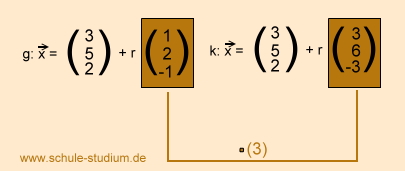
Bsp. 2)
Gleicher Stützvektor, Richtungsvektoren Vielfache voneinander
Wir sehen, dass wenn der Richtungsvektor der einen Geraden ein Vielfaches
der anderen ist, die beiden Geraden parallel sind.
Zusammenfassend liegt eine
parallele und identische Gerade vor, wenn :
 |
der Stützvektor der einen Gerade auf der zweiten Gerade liegt (Punktprobe) und die Richtungsvektoren identisch sind. |
 |
der Stützvektor der einen Gerade auf der zweiten Gerade liegt (Punktprobe) und die Richtungsvektoren Vielfache voneinander sind.
(s. oben Bsp. 1 und Bsp. 2) |
s. auch:
-> Parametergleichungen von Geraden aufstellen, Geradenpunkte ermitteln
-> Vektorielle Darstellung von Geraden im dreidimensionalen Raum
-> Punktproben im 3-dimenionalen Raum
-> Ebenen darstellen aus zwei Geraden
Mathe
Abi Lernhilfen:
(thematisch sortiert ...)
|
|