Aufgabe 1:  
Folgende Gerade ist gegeben:



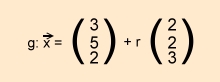
Prüfe rechnerisch, ob die Punkte P1 (1/3/-1) , P2 ( 7/9/8) und P3 (3/2/4)
auf der Geraden liegen.


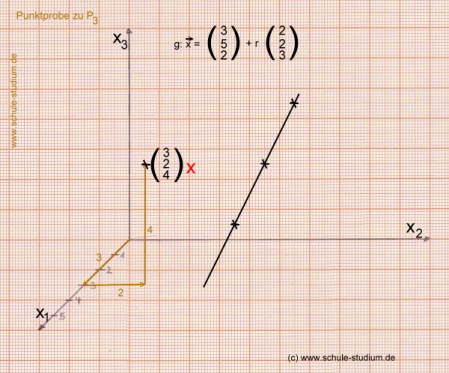
Zur visuellen Veranschaulichung zeichnen wir zunächst die Gerade:




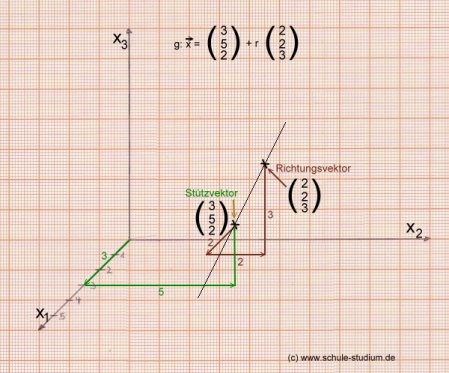
PUNKT P₁:
Liegt der Punkt P₁ (1/3/-1) auf der Geraden ?
Um dies zu überprüfen setzten wir die Gerade gleich dem Ortsvektor.
Der Punkt liegt nur auf der Geraden, wenn es ein ´r´ gibt, dass alle 3 Gleichungen erfüllt.




Wir überprüfen anhand des Koordinatensystems:

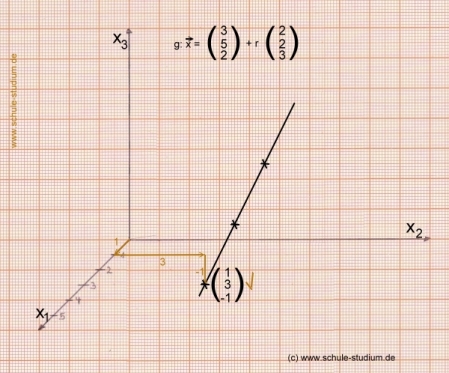
Wir sehen: Der Punkt liegt in der Tat auf der Geraden.

PUNKT P₂:

Liegt der Punkt P₁ (7/9/8) auf der Geraden ?
Um dies zu überprüfen setzten wir erneut die Gerade gleich dem Ortsvektor.
Der Punkt liegt nur auf der Geraden, wenn es ein ´r´ gibt, dass alle 3 Gleichungen erfüllt.




Wir überprüfen erneut anhand des Koordinatensystems:



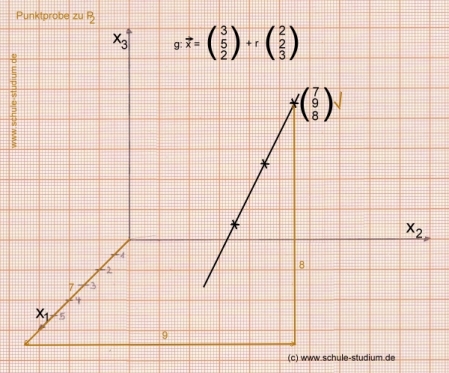
Wir sehen: Der Punkt liegt in der Tat auf der Geraden.



PUNKT P₃:

Liegt der Punkt P₃ (3/2/4) auf der Geraden ?
Um dies zu überprüfen setzten wir erneut die Gerade gleich dem Ortsvektor.
Der Punkt liegt nur auf der Geraden, wenn es ein ´r´ gibt, dass alle 3 Gleichungen erfüllt.


Wir erhalten unterschiedliche Werte für r.
Daraus folgt, dass der Punkt P₃ nicht auf der Geraden liegen kann.




s. auch:

-> Parametergleichungen von Geraden aufstellen, Geradenpunkte ermitteln

-> Vektorielle Darstellung von Geraden im dreidimensionalen Raum

-> Parallele und identische Geraden erkennen

-> Ebenen darstellen aus zwei Geraden


Mathe Abi Lernhilfen:
(thematisch sortiert ...)

	Klett Lambacher Schweizer Lösungsbücher zu Lehrwerken
	Analytische Geometrie und lineare Algebra
	Wahrscheinlichkeitsrechnung
	Analysis (Differential-und Integralrechnung