5./6.
KLASSE
Das
Dualsystem (2er System)
5. Klasse (Gymnasium)
|
Bruchrechnen
- Lernpfad
Bruchzahlen (Brüche und Dezimalzahlen)
(http://www.mathe-online.at/)
- Grundrechenregeln
beim Bruchrechnen
Addition von Brüchen, Subtraktion von Brüchen, Multiplikation
und Division von Brüchen
Klasse 5: Diverse
Klassenarbeiten mit Lösung:
->
Klassenarbeit
1 - Die vier Grundrechenarten Lösung
vorhanden
Zahlenstrahl, Runden & Textaufgaben zur Teibarkeit
und Multiplikation
-> Klassenarbeit
2 - ebene Geometrie Lösung
vorhanden
Gerade, orthogonal, parallel, Quadrat, Parallelogramm
->
Klassenarbeit
3 - Terme und Rechengesetze Lösung
vorhanden
Terme (Summe, Differenz), Rechengesetze
-> Klassenarbeit
4 - Terme und Rechengesetze Lösung
vorhanden
Potenzen und Textaufgaben, Klammerrechnung
-> Klassenarbeit
5 - ebene Geometrie Lösung vorhanden
Parallelen, Orthogonale, Parallelogramm
-> Klassenarbeit
6 - Rechnen mit Größen
aus dem Alltag Lösung vorhanden
Rechnen mit Maßeinheiten, Textaufgaben. G8
-> Klassenarbeit
7 - Römische Zahlen Lösung
vorhanden
Römisches Zahlensystem, Zehnersystem, Runden,
Häufigkeit
-> Klassenarbeit
8 - Römische Zahlen Lösung
vorhanden
Zahlenstrahl, Römische Zahlzeichen, Sachaufgaben,
Diagramme
-> Klassenarbeit
9 - Die vier Grundrechenarten Lösung
vorhanden
schriftliche Addition, Multiplikation und Textaufgaben.
-> Klassenarbeit
10 - Rechnen mit Größen
aus dem Alltag Lösung vorhanden
Maßeinheiten, Zeiten und Längen umrechnen
-> Klassenarbeit
11 - Römische Zahlen Lösung
vorhanden
Runden, Zahlensysteme, Römische Zahlen und Terme.
-> Klassenarbeit
12 - Römische Zahlen Lösung
vorhanden
Natürliche Zahlen, Zahlensysteme, nach Größe
ordnen
-> weitere Klassenarbeiten...
|
7./8.
KLASSE:
|
Prozentrechnung
|
| |
Binomische
Formeln: Fortführung
|
| 8.
KLASSE: |
| |
9./10.
Klasse :
|
Quadratische
Funktionen (Regeln bei der Verschiebung einer Normalparabel)
Lineare
Gleichungssysteme( div. Lösungsverfahren)
Additionsverfahren, Gleichsetzungsverfahren, Einsetzungsverfahren:
|
| 10.
Klasse : |
Zinsrechnen:
(Zinseszins/Ratensparen/Kleinkredit)
Kreisberechnungen:
Wurzelterme und Wurzelgleichungen:
| |
- Wurzelziehen
(teilweises Wurzelziehen, Wurzelziehen bei Kommazahlen, Wurzelziehen
bei Binomischen Aufgaben)
- Wurzelgleichungen
(1): Bestimmen des Definitionsbereiches und
schrittweises Lösen von Wurzelgleichungen
- Wurzelgleichungen
(2): Bestimmen des Definitionsbereiches,
schrittweises Lösen von Wurzelgleichungen & Probe
|
Potenzen
und Potenzgesetze:
| |
- Potenzgesetze
(Addieren, Subtrahieren, Multiplizieren und Dividieren von Potenzen)
|
LOGARITHMUS & EXPONENTIALFUNKTION: (neu)
Trigonometrie: (neu)
|
Oberstufe :
|
Analysis
(Oberstufe)
Funktionen n-ten
Grades: (neu)
|
Themenbereich Geometrie:
|
Geometrie
- Geometrische Grundbegriffe
(Gerade, Halbgerade, Strecke, Kreis, Senkrechte, Parallele)
- griechische Buchstaben
und deren Aussprache für den Geometrieunterricht
- Dreieckskonstruktionen mit Konstruktionsbeschreibung
->
Dreieckskonstruktion ( geg.: Seite
b + c sowie eingeschlossener Winkel)
-> Dreieckskonstruktion (geg.:
Seite a + c sowie eingeschlossener Winkel 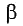 ,
SWS) ,
SWS)
-> Dreieckskonstruktion (geg.:
Seite a + b sowie eingeschlossener Winkel 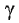 ,
SWS) ,
SWS)
-> Dreieckskonstruktion (geg.:
Seite a + c sowie anliegender Winkel  ,
SSW) ,
SSW)
-> Dreieckskonstruktion (geg.:
Seite b + c sowie anliegender Winkel 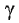 ,
SSW) ,
SSW)
- Winkelberechnungen an Dreiecken
& Vielecken (Nebenwinkel,
Scheitelwinkel, Winkelsummensatz)
- Winkelberechnungen
an Vielecken (Stufenwinkel, Nebenwinkel, Scheitelwinkel,
Wechselwinkel)
- Thaleskreis: Tangenten an
einen Kreis zeichnen
- Die Zentrische Streckung-
RS, Klasse 9
- Dreieckskonstruktion: Thaleskreis (bei
 =
90°) =
90°)
- Dreieckskonstruktion: Thaleskreis (
geg.:b,
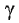 , , 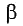 =
90°) =
90°)
- Dreieckskonstruktion:
Thaleskreis ( geg.
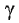 =
90°, c und hc) =
90°, c und hc)
- Konstruktion des Umkreises eines Dreiecks
mit Hilfe der Mittelsenkrechten
- Vierecke und deren Eigenschaften
- Konstruktionsbeschreibungen
in der Geometrie
- Der 1. und 2. Strahlensatz in der
Geometrie (Klasse 9)
- Umwandlung eines Rechteckes
in ein flächengleiches Quadrat mit Hilfe des Höhensatzes.
- Umwandlung
eines Quadrates in ein flächengleiches Rechteck (Methode
1, Bsp.1)
- Umwandlung
eines Quadrates in ein flächengleiches Rechteck (Methode
2, Bsp.2)
|
| |



